draw spiral curve civil 3d

Archimedean spirals are often used in the analysis of inductor coils, spiral heat exchangers, and microfluidic devices. Today, we will demonstrate how to build an Archimedean screw using analytic equations and their derivatives to define a set of spiral curves. Based on these curves, we will and so create a 2nd geometry with specific thickness, extruding it to a total 3D geometry.

A Brief Introduction to Archimedean Spirals

Widely observed in nature, spirals, or helices, are utilized in many engineering science designs. As an electrical engineer, for instance, yous may wind inductive coils in spiral patterns and design helical antennas. Every bit a mechanical engineer, you lot may apply spirals when designing springs, helical gears, or even the lookout man machinery highlighted below.

An example of an Archimedean spiral used in a clock machinery. Image by Greubel Forsey. Licensed by CC Past-SA 3.0, via Wikimedia Eatables.

Here, we'll focus on a specific blazon of screw, the i that is featured in the mechanism shown above: an Archimedean spiral. An Archimedean spiral is a type of a spiral that has a fixed distance between its successive turns. This property enables it to be widely used in the design of flat coils and springs.

Nosotros can depict an Archimedean spiral with the following equation in polar coordinates:

r=a+b\theta

where a and b are parameters that ascertain the initial radius of the screw and the distance between its successive turns, the latter of which is equal to two \pi b. Annotation that an Archimedean spiral is as well sometimes referred to equally an arithmetic spiral. This name derives from the arithmetic progression of the distance from the origin to point on the aforementioned radial.

Designing a Parameterized Archimedean Screw Geometry

At present that nosotros've introduced Archimedean spirals, permit'due south take a look at how to parameterize and create such a pattern for assay in COMSOL Multiphysics.

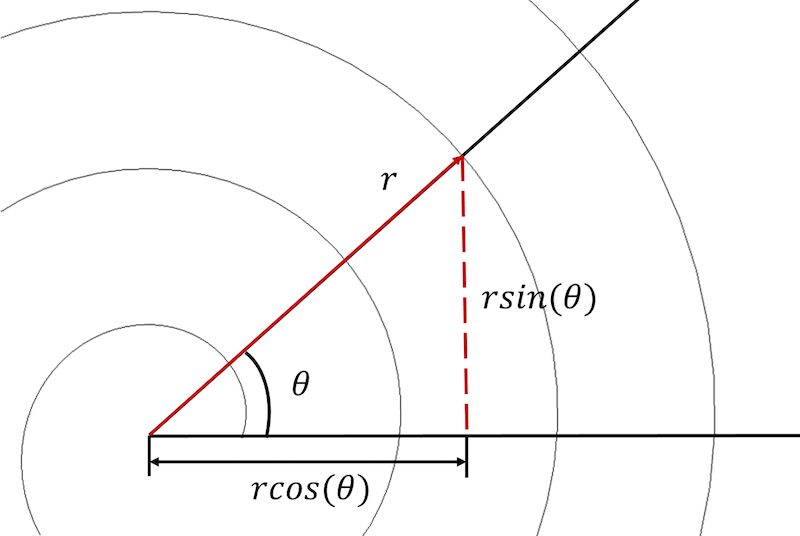
An Archimedean spiral tin exist described in both polar and Cartesian coordinates.

To begin, we need to convert the spiral equations from a polar to a Cartesian coordinate system and express each equation in a parametric form:

\begin{align*}
x_{component}=rcos(\theta) \\
y_{component}=rsin(\theta)
\end{align*}

This transformation allows us to rewrite the Archimedean spiral's equation in a parametric grade in the Cartesian coordinate system:

\brainstorm{align*}
x_{component}=(a+b\theta)cos(\theta) \\
y_{component}=(a+b\theta)sin(\theta)
\end{marshal*}

In COMSOL Multiphysics, it is necessary to decide on the ready of parameters that will define the spiral geometry. These parameters are the spiral's initial radius a_{initial}, the spiral'southward final radius a_{final}, and the desired number of turns n. The screw growth rate b can then exist expressed as:

b=\frac{a_{final}-a_{initial}}{2 \pi n}

Farther, we need to decide on the spiral's start bending theta_0 and end angle theta_f. Let'due south begin with the values of theta_0=0 and theta_f=2 \pi n. With this information, we are able to define a gear up of parameters for the screw geometry.

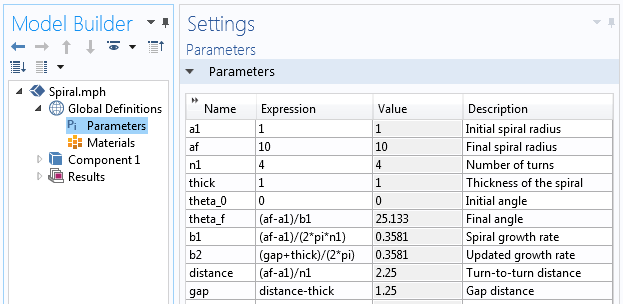
The parameters used to build the spiral geometry.

To build this spiral, nosotros'll start with a 3D Component and create a Work Plane in the Geometry co-operative. In the Work Plane geometry, nosotros and then add together a Parametric Curve and apply the parametric equations referenced above with a varying angle to draw a second version of the Archimedean spiral. These equations tin can exist directly entered into the parametric curve'due south Expression field, or we can first define each equation in a new Analytic function every bit:

\begin{align*}
X_{fun}=(a+bs)cos(southward) \\
Y_{fun}=(a+bs)sin(s) \\
\cease{marshal*}

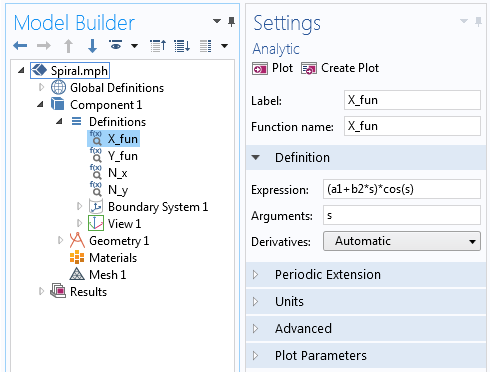
The X-component of the Archimedean spiral equation divers in the Analytic function.

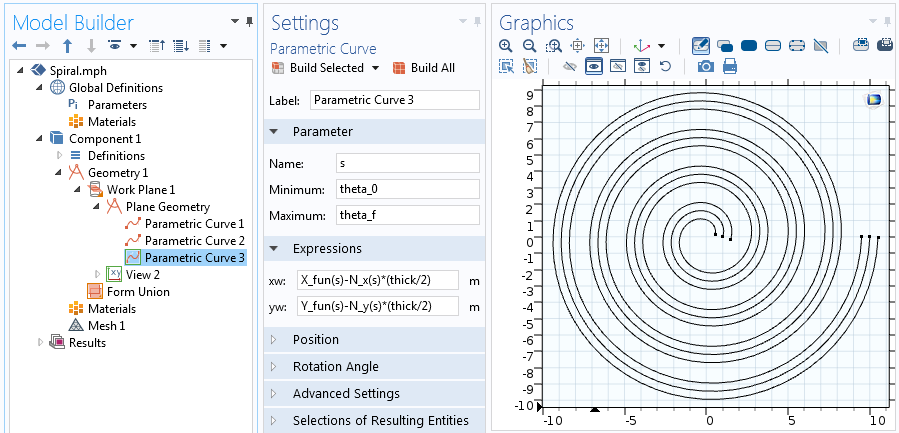
The Analytic role can be used in the expressions for the Parametric Bend. In this Parametric Curve, we vary parameter s from the initial angle of the spiral, theta_0, to the terminal angle of the spiral, theta_f=2 \pi n.

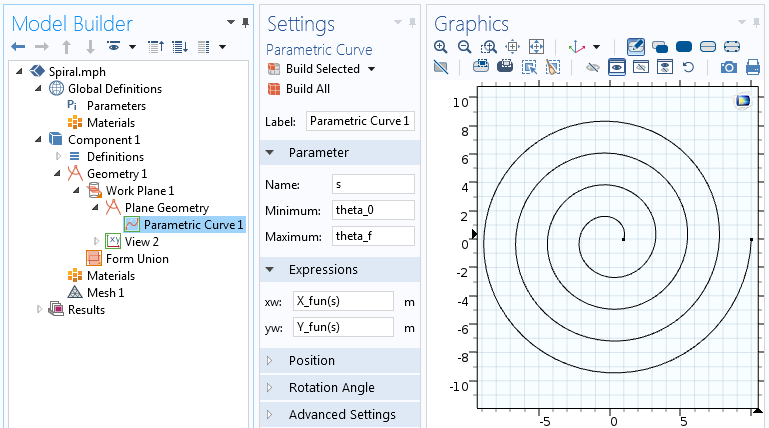
The settings for the Parametric Curve feature.

The parametric screw equations used in the Parametric Curve feature will result in a screw represented past a curve. Let'south at present build upon this geometry, adding thickness to information technology in order to create a 2D solid object.

Up to this indicate, our spiral has been parameterized in terms of the initial radius a_{initial}, final radius a_{final}, and desired number of turns n. Now, nosotros must incorporate thickness as another control parameter in the spiral equation.

Permit'southward begin with the main property of the spiral, which states that the altitude between the spiral turns is equal to ii \pi b. This is as well equivalent to \frac{a_{final}-a_{initial}}{north}. To incorporate thickness, we stand for the distance between each successive plough of the spiral every bit a sum of the screw thickness and the remaining gap between turns, thick+gap.

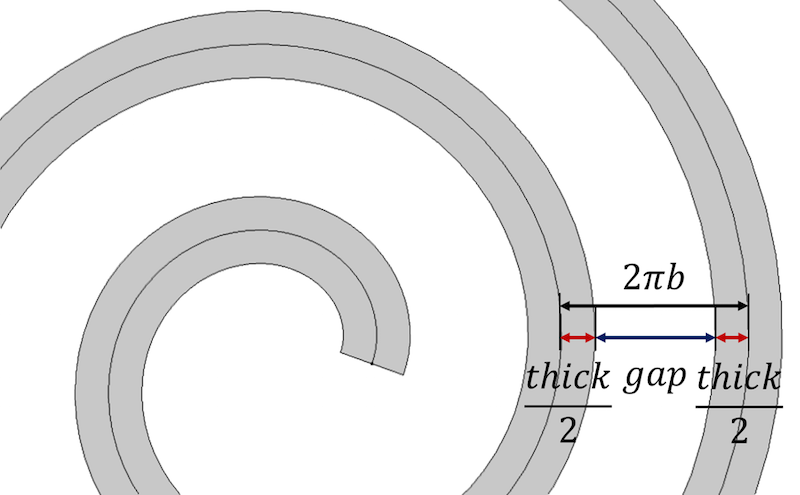
The altitude betwixt spirals turns is defined in terms of the screw thickness and gap parameters.

To control thickness and obtain identical altitude between the turns, the altitude can be expressed equally:

\begin{align*}
distance=\frac{a_{initial}-a_{last}}{n} \\
gap=distance-thick
\end{align*}

After defining thickness and expressing the gap betwixt turns in terms of thickness and constant distance between centerlines of the spiral, we tin rewrite the spiral growth parameter in terms of thickness as:

\begin{marshal*}
altitude=2\pi b \\
b=\frac{gap+thick}{2\pi}
\terminate{align*}

We will likewise want to express the final bending of the spiral in terms of its initial and last radii:

\begin{marshal*}
\theta_{last}=2 \pi n \\
a_{final}=\text{total distance}+a_{initial} \\
a_{final}=2 \pi bn+a_{initial} \\
n=\frac{a_{terminal}-a_{initial}}{2 \pi b} \\
\theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{ii \pi b} \\
\theta_{final}=\frac{a_{final}-a_{initial}}{b}
\end{align*}

Want to outset the spiral from an bending other than zero? If and so, you volition demand to add this initial angle to your final bending in the expression for the parameter: theta_f=\frac{a_{last}-a_{initial}}{b}+theta_0.

Duplicating the existing spiral curve twice and placing these curves with an get-go of -\frac{thick}{2} and +\frac{thick}{2} with respect to the initial spiral curve allows us to build the spiral with thickness. To position the upper and lower spirals correctly, we must make certain that the offset spirals are normal to the initial spiral curve. This can be achieved past multiplying the showtime distance \pm\frac{thick}{ii} by the unit vector normal to the screw bend. The equations of the normal vectors to a curve in parametric grade are:

n_x=-\frac{dy}{ds} \quad \text{and} \quad n_y=\frac{dx}{ds}

where southward is the parameter used in the Parametric Curve feature. To become a unit normal, we need to divide these expressions by the length of the normal:

\sqrt{(dx/ds)^2+(dy/ds)^2 }

Our updated parametric equations for the Archimedean screw with a half-thickness shift are:

\begin{marshal*}
x_{component}=(a+bs)cos(due south)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^two}}\frac{thick}{2} \\
y_{component}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{ii}
\stop{align*}

Writing out these equations in the parametric bend's expression fields can be rather time consuming. As such, we innovate the following notation:

\begin{align*}
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^ii+(dy/ds)^2}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\terminate{align*}

where each N_x and N_y is defined via the Analytic function in COMSOL Multiphysics, similar to how we defined X_{fun} and Y_{fun} for the beginning parametric curve. Inside the function, we utilize the differentiation operator, d(f(ten),x), to take the derivative, as depicted in the following screenshot.

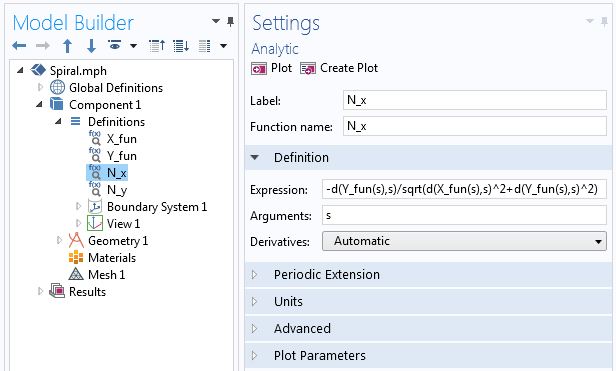
Examples of the derivative operator used in the Analytic office.

The functions X_{fun}, Y_{fun}, N_x, and N_y can then be used directly in the parametric curve's expressions for the bend on one side:

\begin{align*}
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(south)+N_y(due south)\frac{thick}{ii}
\end{align*}

The functions can also exist used for the curve on the other side:

\begin{align*}
x_{upper}=X_{fun}(due south)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(south)-N_y(s)\frac{thick}{ii}
\cease{marshal*}

Equations for the second of the ii commencement parametric curves.

To join the ends of ii curves, we add ii more parametric curves using a slight modification of the equations mentioned to a higher place. For the bend that joins the center of the spiral, we accept to evaluate X_{fun}, Y_{fun}, N_x, and N_y for the starting value of the angle, theta. For the curve that joins the outer side of the spiral, we have to evaluate the last value of theta. Therefore, the joining bend in the middle is:

\begin{align*}
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\
Y_{fun}(theta_0)+south\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}

The outer joining bend, meanwhile, is:

\begin{align*}
X_{fun}(theta_f)+southward\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+due south\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}

In both of the above equations, s goes from -1 to +1, as shown in the screenshot below.

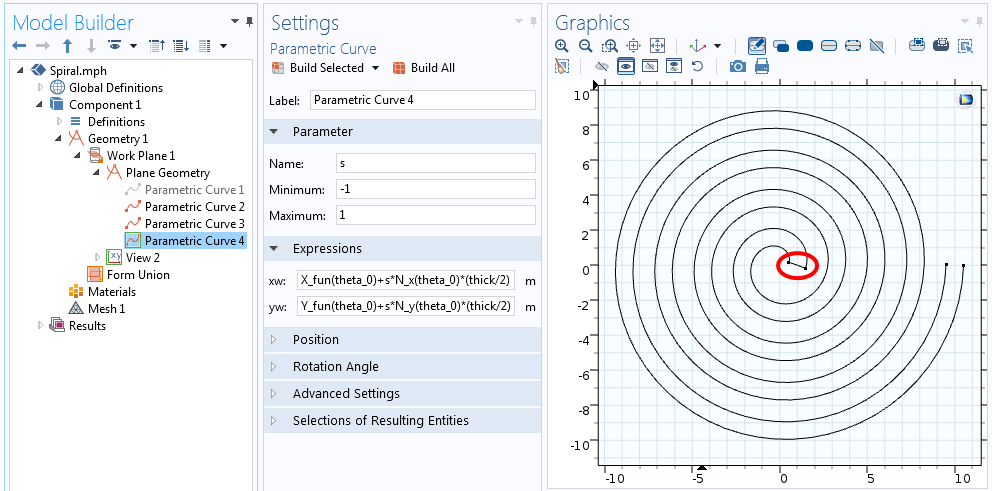
Equations for the curve that joins 1 terminate of the screw.

We now have five curves that ascertain the centerline of the spiral and all 4 sides of the contour. We can disable (or even delete) the curve describing the centerline since information technology isn't truly necessary, leaving just the spiral outline. With the outline of our screw defined, the Catechumen to Solid operation can exist used to create a single geometry object. This 2D screw can finally be extruded into 3D via the Extrude operation.

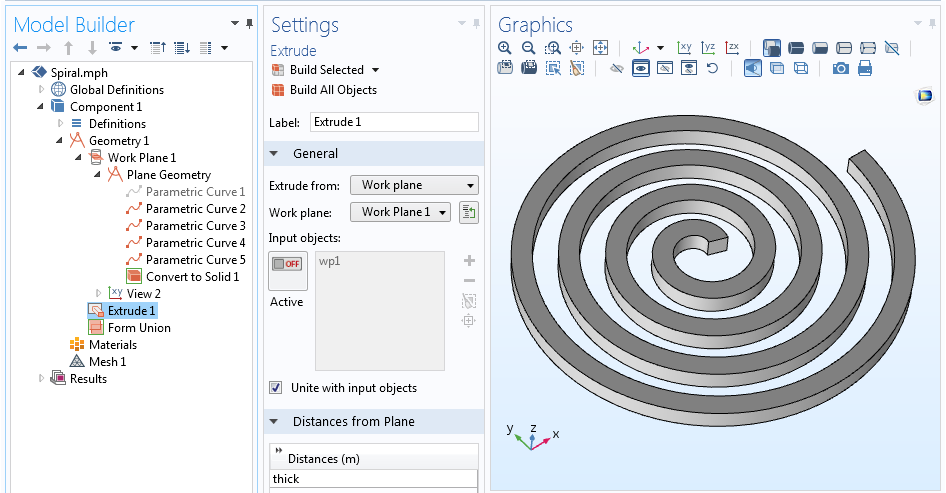
The full geometry sequence and extruded 3D spiral geometry.

Closing Remarks on Modeling Archimedean Spirals in COMSOL Multiphysics

We take walked y'all through the steps of creating a fully parameterized Archimedean spiral. With this spiral geometry, you tin can modify any of the parameters and experiment with different designs, or even use them as parameters in an optimization study. We encourage you lot to utilize this technique in your own modeling processes, advancing the analysis of your particular spiral-based technology pattern.

Further Resources on Designing and Analyzing Spirals

• To explore farther applications of simulation in the design of screw models, try out this tutorial model: Spiral Slot Antenna
• Read a related user story: "Assay of Screw Resonator Filters"

phillipsbetion.blogspot.com

Source: https://www.comsol.com/blogs/how-to-build-a-parameterized-archimedean-spiral-geometry/

Share this post